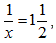Q 4.
(a) Using a scale of 2 cm to 1 unit on both axes, draw two perpendicular axes, Ox and Oy on a graph sheet.
(b) On the same graph sheet, mark the x-axis from −5 to 5 and the y-axis from −6 to 6.
(c)
(i) Plot on the same same graph sheet the points A(1, 1½), B(4, 1½), C(1, 4).
(ii) Join the points to form a triangle. What type of triangle have you drawn?
(d) Draw A1 B1 C1 of ABC under a reflection in the y-axis where A → A1, B → B1, and C → C1. Label the vertices and coordinates clearly.
(e) Draw the image A2 B2 C2 of ABC under an enlargement with scale factor -1 with the centre of the enlargement as the origin. (0, 0) where A → A2, B → B2, and C → C2. Show the lines of enlargement and label the vertices and coordinates clearly.
(f) What single transformation maps A1 B1 C1 unto A2 B2 C2 where A1 → A2, B1 → B2, and C1 → C2
Q 5.
(a) The data below shows the distribution of the ages of workers in a factory.
| Age (in years) | No. of workers |
| 19 | 3 |
| 24 | 7 |
| 29 | 8 |
| 34 | 4 |
| 39 | 5 |
| 44 | 3 |
(i) How many workers are there in the factory?
(ii) What is the modal age of the distribution?
(iii) Calculate the mean age of the workers, correct to one decimal place.
(b)
(i) Make T the subject of the relation ![]()
(ii) If I = ¢64,000.00 and R = 25%, find the value of T in years.